複素数 の 範囲 と は
ケア プラン 軽微 な 変更複素数の範囲での因数分解の例題4問 | 高校数学の美しい物語. ストロガッツ 非線形 ダイナミクス と カオス pdf
ばね の 伸び 計算複素数の範囲で因数分解する方法. まずは,2次式 ax^2+bx+c ax2 +bx +c を複素数の範囲で因数分解することを考えます。. 実は,二次方程式 ax^2+bx+c=0 ax2 +bx+c = 0 の解を x=alpha,beta x = …. 【基本】二次式を複素数の範囲で因数分解する | なかけんの . 解と係数の関係と因数分解. 二次方程式 a x 2 + b x + c = 0 の解を α, β とします。. 複素数の範囲では、必ず解が存在します(参 …. 複素数 - Wikipedia. うさぎでもわかる複素解析 Part1 複素数の基礎・複素数平面 . 複素数 の 範囲 と は複素数とは?公式や i の 2 乗の意味、計算問題の解き …. 複素数 の 範囲 と は複素数とは、 数直線上に表せる数(実数)と表せない数(虚数)を合わせた数の概念 です。 まずは、複素数を知る上で必要不可欠な「虚数単位 (i)」について見ていきましょう。. 複素数とは?「二乗すると-1」になる数って? - クマの数学日記. 少なくとも実数の範囲では 、ですが。 この記事では、「二乗すると−1になる数」を考えることで、なにが嬉しいのか、を説明して …. 複素数 | 高校数学の美しい物語. 複素数平面において正三角形となる条件. 複素数 alpha,beta,gamma α,β,γ に対応する複素数平面上の三点 A (alpha), B (beta), C (gamma) A(α),B(β),C (γ) が正三角形となる必要十分条件は,. (alpha-beta)^2+ (beta …. 複素数 の 範囲 と は複素数平面の公式まとめ(極形式・回転・ドモアブル …. 1. 複素数 の 範囲 と は複素数平面. まずは複素数の復習からしていきましょう。 1.1 複素数と実数・虚数(復習) 「( i^2 = -1 )」となる数 ( i ) を 虚数単位といいます。 さらに,( a + bi )(( a, b ) は実数)の形で表される数を 複素数といいます。 【例】 …. 複素数の定義と計算 - 高校数学.net. (small{ displaystyle frac{1+2i}{1+i} })のような形の複素数は、(small{ 1-i })を分母と分子にかけて、 分母を有理化して基本形に変形しよう。 (small{begin{eqnarray} displaystyle …. 複素数の基礎 ~ 性質と例題 ~ - 理数アラカルト. 複素数 の 範囲 と は定義. 虚数 i i を i2 = −1 i 2 = − 1 を満たす数と定義するときに、 実数 x,y x, y によって、 と表される数 z z を 複素数 という。 ここで x x を複素数 z z の実部 (実数部分)といい、 と表す。 また、 y y を複素数 z z の虚部 (虚 …. 2次式と複2次式の複素数の範囲での因数分解 - 受験の月. 高校数学総覧. 高校数学Ⅱ 複素数と方程式. 複素数 の 範囲 と は2次式と複2次式の複素数の範囲での因数分解. 2020.06.01. 複素数 の 範囲 と は検索用コード. 複素数 の 範囲 と は2次方程 …. 複素数の存在意義と様々な例 | 高校数学の美しい物語. 足首 の しびれ
家庭 用 ヒートポンプ 給湯 機 の 据付け ガイド ブック代数学の基本定理. 複素数係数の n n 次方程式は,複素数の解を(重複度込みで) n n 個持つ. 方程式の解は実数の範囲だと存在しな …. 因数分解(複素数範囲) | 教えて数学理科. 因数分解 (複素数範囲) | 教えて数学理科. 複素数 の 範囲 と は複素数の範囲まで拡張された因数分解について見ていきます。 (例題) x4 + 2x2 − 15 を、 …. 【基本】複素数 | なかけんの数学ノート. おわりに. 数の範囲の拡大と複素数. 【基本】実数の分類 でも紹介しましたが、今まで数の範囲がどんどん広がってきましたね。 足し …. 複素数の定義と基本的性質 – gleamath.com. 複素数 の 範囲 と は高校数学 By gleamath. 実数の範囲では, 2乗して負になる数は存在しない.. すなわち, a > 0 とするとき, 2次方程式. 複素数 の 範囲 と はx2 = −a. は解を持たない.. おなか の 中 に 鬼 が いる パネルシアター
約束 の ネバーランド 似 た 漫画 …. 【基本】二次方程式の解と複素数 | なかけんの数学ノート. 複素数 の 範囲 と は実数の範囲では,、0以上の場合は平方根を考えることができますが、負の場合は考えられません。 しかし、 複素数の範囲まで数の …. 数学Ⅱ|複素数範囲での因数分解のやり方とコツ | 教科書より . 複素数 の 範囲 と は数学Ⅱ|複素数範囲での因数分解のやり方とコツ | 教科書より詳しい高校数学. ホーム. 数学Ⅱ:複素数と方程式. 複素数範囲での因 …. うさぎでもわかる線形代数 応用編第1羽 複素数とベクトル . 成分が複素数のベクトル ( vec{a} ), ( vec{b} ) の複素内積の計算法則は次の通りである。 ( vec{a} cdot vec{b} = overline{vec{b} …. 複素数 の 範囲 と は複素数の範囲で因数分解をする / 数学II by OKボーイ |マナペディア|. 複素数 の 範囲 と は実数解の範囲であれば、D<0ですので 解なし となる点に注意しましょう。 ・ 負の平方根の計算問題. キッチン の 色 人気
再婚 相手 と 子供 が うまくいかない・ 複素数の計算 [複素数の簡単な乗法] ・ 複 …. 複素数の性質 | 高校数学の知識庫. 複素数 の 範囲 と はz = a + b i. 複素数 の 範囲 と はです。 これを使って色々な性質を見ていきます。 というよりもこれがあれば全ての公式は簡単にわかります。 やってみま …. 複素数の範囲とは何ですか?? あと、いきなりiご出てきたのは . 複素数の範囲とは何ですか? あと、いきなりiご出てきたのはどうしてですか? - Clearnote. Clearnote. Q&A. 複素数 の 範囲 と は高校生. 数学. 複素 …. 複素数 の 範囲 と は「どこまで因数分解するか?」係数の範囲は有理数、実数 . ここで、多項式の係数の範囲として、有理数全体 (mathbb{Q})、実数全体 (mathbb{R})、複素数全体 (mathbb{C})、 …. 【複素数とはなにか】仮想の数、究極の数|蛸文(たこふみ). 虚数とは i で表され、二乗すると -1 となる数である。. i^2 = -1. そして、複素数とは実数の部分 (実部)と虚数の部分 (虚部)の足し算の形 …. 複素関数論(複素解析)まとめ | 高校数学の美しい物語. 1. 複素数の指数関数. 複素数 z=a+bi z = a +bi に対して,指数関数 e^z ez は以下の式で定義される: e^ { (a+bi)}=e^a (cos b+isin …. 【初見で9割が間違える?!】複素数とは? ルートの掛け算 負 . 「いいね」が215件、コメントが20件。「【初見で9割が間違える?!】複素数とは? ルートの掛け算 負の数の平方根に注意! 【 …. 運動中とその後の心拍数を適正に保つには.オンラインストア . エクササイズ中や、エクササイズ後の心拍数は一定範囲内に保ちたい。その最初のステップとして、安静時の心拍数と最大心拍数 …. 一夜で水槽が空っぽに 消えたメダカ400匹“犯人”正体は?. 「400匹のメダカ」が飼われていた水槽ですが、一夜にして消えてしまいました。 犯人は?消えたメダカ400匹 メダカが消えたのは11日、名 …. 複素数の偏角の求め方と公式 - 具体例で学ぶ数学. 偏角の求め方. 複素数 の 範囲 と はz = 1 + i z = 1 + i の偏角を求めてみましょう。. 複素数平面で 1 + i 1 + i は、図の z z に対応します。. 複素数 の 範囲 と はこのとき、図の θ θ は 45∘ 45 ∘ になるので、偏角は 45∘ 45 ∘ です。. 複素数 z z の偏角を argz a r g z と書くことが多いです。. つまり、上記の . 複素関数論(複素解析)まとめ | 高校数学の美しい物語. 複素関数論(複素解析))は,複素数上で定義された関数の微積分など扱う分野です。 複素関数の微積分の基本,美しい複素積分の理論(コーシーの積分定理・ローラン展開・留数定理),楽しい応用など,順々に紹介していきます。. 【5分でわかる】交流の複素数とは?必要な理由を …. 複素数 の 範囲 と は実数と虚数とは? 少し数学っぽいお話になってしまいますが、複素数というのは実数と虚数というものを組み合わせたものです。 そのため、まずは実数と虚数がどのようなものかを知る必要があります。 実数と虚数にはそれぞれ下記の特徴があります。. 複素数の範囲で解くとはどういうことですか? - Yahoo!知恵袋. 腰 を 丸める 痛い
鶴ヶ峰 住み やす さ複素数の範囲で解くとはどういうことですか? また(1)が1で代入したら0なのに答えが出ません 答えを見たところ-1で代入してますが-1だとP(x)が成り立ちません、 どういうことですか??本当に悩んでるので教えてください. 複素数を学ぶ | 高校数学の知識庫. 複素数とは さて、実数ではなく、 2 乗すると-1 になる数字=”虚数単位”を含む数字の虚数を学習しましたが、実数と虚数は数字であることに変わりありません。 私たちは実数 と一括りに言いますがその実数の中にも有理数や無理数というわけ方があり、さらに整数、自然数・・・というよう . 複素対数関数の主値Log zとは、計算例 | 趣味の大学数学. 以上、複素関数の対数関数(mathrm{Log,} z)、主値とは何かを紹介してきました。僕は複素解析を学び初めの頃、対数の主値の考え方がイマイチ理解できませんでした。それは例えば、実数のケースと異なり、(e^{z}=1)のような方程式. 【高校数学Ⅲ】極形式(複素数の極座標表示) | 受験の月. 複素数 の 範囲 と は極形式(複素数の極座標表示). 後半の問題は難度が高く優先度は低いので、初学者はスルー推奨である。. 複素数 の 範囲 と は複素数平面は原点中心の回転を成り立ちとしているから, 極座標との相性がよい. 偏角は, $0θ<2π$の範囲でただ1通りに定まる. 一般には, $ {arg z=θ+2nπ . サッとわかる複素数のn乗根の計算方法とイメージ→円を意識し . 複素数のn乗根と実数のn乗根の比較 複素数の理解を深めるために、実数の(n)乗根も考えてみましょう。 これまで実数範囲で1の6乗根を考えろ、と言われると(pmsqrt[6]{1}=pm1)の解のみしか考えられませんでした。 他にも2の3乗根など . 複素数 の 範囲 と は複素関数とは?|定義と具体例の解説【複素解析】 – 高校物理 . 複素数の世界では、三角関数はどのように表されるのでしょうか?今回は複素数の世界での三角関数、複素三角関数の定義と公式、そして例題について解説します。複素三角関数の不思議な性質について見ていきましょう。. 【高校数学Ⅲ】円周上を動く複素数の絶対値と偏角の範囲 . 複素数の等式が表す三角形の形状決定 3点が正三角形を作る条件と三角形の相似条件 複素数平面上の直線の方程式(垂直二等分線と円の接線の方程式) 複素数平面上の円の方程式(アポロニウスの円) 円周上を動く複素数の絶対値. 複素数 の 範囲 と は複素数平面について、定義から難しい公式まで16個の知識 - 具体 . 複素数 の 範囲 と は例えば、$(2+3i)$ という複素数は、原点から右に $2$、上に $3$ 移動した点に対応します。全ての複素数が、平面上の1つの点に対応します。 複素数平面のことを ガウス平面 と呼ぶことがあります。 また、横軸を 実軸 、縦軸のことを 虚軸 と呼び …. オイラーの公式と複素指数関数 | 高校数学の美しい物語. ヘア カラー タオル に 色 が つく
風呂 の 蓋 代用とても有名な オイラーの公式 ・ オイラーの等式 について高校数学の範囲 でわかるように説明します。 目次 オイラーの公式とオイラーの等式 複素数の指数関数(複素指数関数) オイラーの公式は美しい? オイラーの公式の証明 . 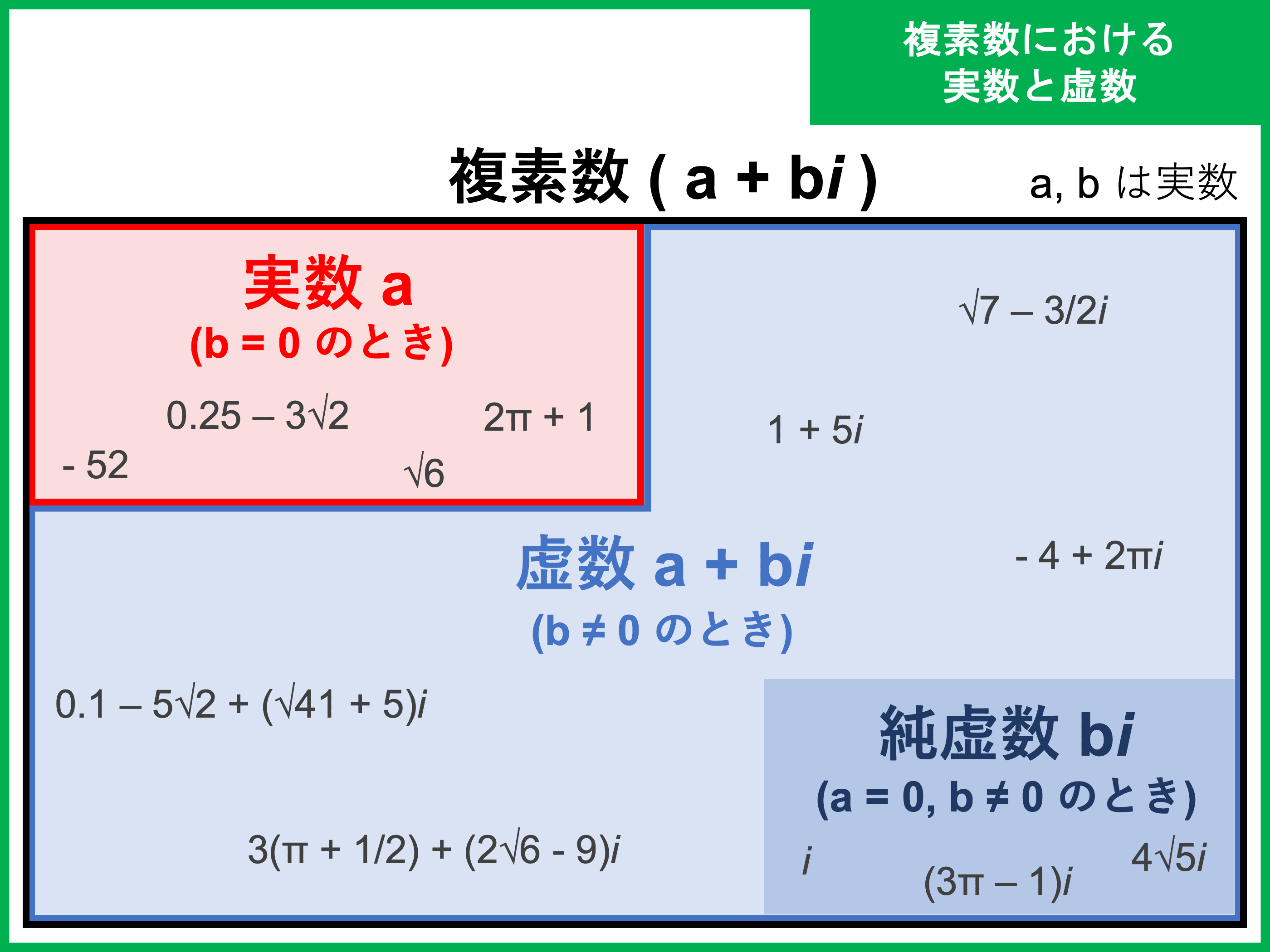
宮戸 島 月 浜 の みんなの 家3乗の和や差は因数分解できます。. a3 +b3 = (a + b)(a2 − ab + b2) a3 −b3 = (a − b)(a2 + ab + b2) プラスやマイナスの符号がどこについているのかよく . 複素数の性質 | 高校数学の知識庫. ド・モアブルの定理とは 数学Ⅲの複素数平面において重要な公式の1つが ド・モアブルの定理 です。これは何かというと簡単にいえば 複素数の累乗に関する定理 です。この公式を知っていると累乗の計算が圧倒的に楽になります。. 複素数の範囲で因数分解をする / 数学II by OKボーイ |マナペディア|. よって、この方程式の解は となります。 つまり が答えとなります。 今回は、 複素数の範囲で因数分解しなさいという問題でしたのでここまでやりました。実数解の範囲であれば、D<0ですので 解なしとなる点に注意しましょう。. 複素数平面を総まとめ!数IIIで習う性質・公式一覧 | 受験辞典. 数III「複素数平面」について、さまざまな公式や性質を図形を示しながらわかりやすくまとめています。 関連記事へのリンクも示しているので、ぜひ複素数平面の理解に役立ててくださいね! 目次複素数平面とは?共役複素数複素数 . 電験三種~数学のレベルと試験でどう使われるか~│電気の . 電験三種では数学が必ず求められます。この記事では、電験三種で求められる数学の知識、必要な数学の公式(分数、一次方程式、連立方程式、二次方程式、平方根、指数、三角関数、複素数、ベクトル、対数)と実際の問題で求められる数学がどのように使われているのか、どう数学の勉強を . 複素数の平方根(ルート)を求める公式と使用例 | 数学の星. 平方根 (ルート)とは. 複素数aがbの平方根であるというのは、 が成立していると言うことです。. 逆に、二つの複素数 が という関係を満たしている時、複素数 は の平方根と呼びます。. 複素数 の 範囲 と は通常、平方根 (ルートの記号√)は正の実数もしくは0に対して使 …. 複素数の極形式 | おいしい数学. 複素数の極形式での積と商. 2 つの極形式で表した複素数 z1 = r1(cosθ1 + isinθ1) , z2 = r2(cosθ2 + isinθ2) の積は 三角関数の加法定理 を使うと. 複素数 の 範囲 と は= r1r2{cos(θ1 + θ2) + isin(θ1 + θ2)} となり, 大きさはかけられ,偏角は足される ことがわかります.. = r1 r2{cos(θ1 − …. 【最強のわかりやすさ】インピーダンスの複素数表示 …. 電気の基本知識 2023.03.21 当サイトはアフィリエイト広告を利用しています。 【最強のわかりやすさ】インピーダンスの複素数表示とは?簡単に解説 交流のインピーダンスは複素数として表示することができます。 インピーダンスを複素数で表示すると、回路の計算がとても簡単に …. 因数分解(複素数範囲) | 教えて数学理科. 因数分解 (複素数範囲) 複素数の範囲まで拡張された因数分解について見ていきます。. x4 + 2x2 − 15 を、因数の係数が (ア)有理数 (イ)実数 (ウ)複素数 の各場合について因数分解せよ。. 複2次式の因数分解です。. の2パターンがありますが、この問 …. 複素数平面【複素数平面】. L 複素数平面 数学Ⅱで学んだように, 以下,複素数 D EL と書いた場合,文字 D,E は実数を表すものとする。 複素数は つの実数 D,E と虚数単位 L を用いて D EL の形で表される。 複素数 D EL について,D をその実部といい,E をその虚部という。. [数2]複素数とは?実部、虚部、虚数と虚数単位をわかりやすく . 複素数とは?のまとめ 複素数について解説しました。ポイントは下記の3つです。 複素数はa,bを実数として、a+biで表される数です。複素数には実数と虚数が含まれます。 2乗して-1となる数をiとし、これを虚数単位といいます。iが含まれる. 複素数の偏角 - Wikipedia. 複素数平面での複素数の絶対値 r, 偏角 φ。 数学において、複素数の偏角(へんかく、英: argument of complex )とは、複素数平面上で複素数が表す点の動径が表す一般角のことである。 複素数 z の偏角は記号で arg z で表す。 で表す。. 複素数と方程式|2次式の因数分解について | 日々是鍛錬 ひびこ . このことは、あとで学習する 剰余の定理 や 因数定理 と関わってくるので覚えておくと良いでしょう。 また、 係数が実数 である2次式であれば、 複素数の範囲で 常に1次式の積に因数分解できることも覚えておきましょう。 「 複素数の範囲で 」という文言に注意しましょう。. 複素数 の 範囲 と は複素フーリエ級数を分かりやすく解説!【なんとなく学ぶ . この式は複素数の概念を使っているので、普通の関数と区別して「複素関数」と言います。 とりあえず今はこの公式が成り立つものだとして話を進めていきましょう。このオイラーの公式を使うと、先ほどのフーリエ級数を次の図のような「 複素フーリエ級数 」に変形することが出来ます。. 複素数でargとは?ガウス平面の偏角? | 令和の知恵袋. まとめ:複素数でargとは?. ガウス平面の偏角?. 複素数平面のargは、複素数が表す点の動径が表す一般角のこと。. 複素数 の 範囲 と は実軸の正の向きから反時計回りに何度回ったかを表す角。. 例えば、複素数z=1+iの偏角はarg (1+i)=π/4である。. 複素数 の 範囲 と はこれは、複素数z=1+iが表す点は . 虚数(複素数)の存在の立場を詳しく解説しました! | ます . 虚数(複素数)とは何かの理解の仕方 虚数(複素数)の理解の仕方を伝えます。この回答は次の通りです。 虚数が現実世界に存在するかを探索することは諦めて、 (①や②の考え方は諦める) ただ単に、その存在を認めることです。. 複素数の指数関数・対数関数・べき関数 - 新潟大学. このページの最後に、複素数の指数や対数についての性質をいくつかまとめておく。実数のときと同じ式が成り立つこともあればそうでないこともあるので、複素数の指数や対数が現れる計算ではいつも丁寧な計算を行うように心がけよう。. 複素数 の 範囲 と は虚数・虚数単位って一体なに?複素数の考え方と基礎知識 . 複素数の極形式r (cosθ+i sinθ)を用いると,複素数の積・商を簡単に求めることができます.この記事では,具体例を用いて極形式を用いた掛け算・割り算の計算を説明します.. 実数は2乗すると0以上の実数となりますが,2乗して−1となる数を「虚 …. 複素数 の 範囲 と は複素数:実数と虚数、公式、iの二乗、計算の方法 | Hatsudy . 高校数学で学ぶ内容の一つが複素数です。複素数というのは、虚数(i)(Imaginary number)を含む数を指します。そのため、複素数も虚数も同じ概念と理解すればいいです。実数と虚数を合わせた数字が複素数です。虚数を利用して計算するためには、虚数の概念を学ばなければいけません。. 複素素数の分布と性質. そうして、複素数範囲での素数である『複素素数』についての研究を始めた。 2. 研究方法① 実部、虚部を整数と定める。複素素数の定義『±1,±i以外のいかなる数でも割り切れない複 素数範囲での数を素数とする。』に従って素数で. 複素解析 - 北海道大学. 1.1 複素関数の導入 複素関数とは複素数z を変数とする関数のことで, w = f(z) 等として表す. z の 動く範囲をf(z) の定義域, そのときのw の動く範囲を値域と呼ぶ. z = x+iy とおけば, f(z) は2 つの実変数x,y の関数となる. f(z) の実部および u(). 複素数の絶対値 | おいしい数学. 複素数の絶対値の性質 $|alpha|$ に関する性質を整理します.今後複素数の計算を $overline{alpha}$ と $|alpha|$ を使うことで済ましてしまうことが多々ありますが,以下の性質をよく使います. 証明は極形式を使用した方法が楽なので,そこまで待ってもいいと思います.. 複素数 の 範囲 と は【導入】複素数を考える意味について | なかけんの数学ノート. 複素数と方程式 上では、複素数と回転について書きましたが、数学的な意味で言えば、 複素数は方程式を考える上で重要な意味を持っています。ここでは、その点について書いていきます。 小学校時代の算数から、数の範囲はだんだん広がってき …. 解と係数の関係:複素数を含む因数分解や解の存在範囲 - Hatsudy. 複素数を含む因数分解であっても可能です。それに加えて、解と係数の関係を利用して二次方程式を作ることもできます。それに加えて、解の存在範囲を把握できるようになりましょう。解と係数の関係は実数解を得る条件としても利用され. 収束半径の意味と求め方 | 高校数学の美しい物語. 収束半径の意味と求め方. べき級数 displaystylesum_ {n=0}^ {infty}a_nz^n n=0∑∞ anzn に対して,以下の1,2を両方満たす rho ρ (ただし 0leq rho leqinfty 0 ≤ ρ ≤ ∞ )が存在する:. このような rho ρ をべき級数の 収束半径 と言います。. この記事では z z は複素数 . 複素数と方程式|高次式の因数分解|数学Ⅱ|定期テスト対策サイト. ここで紹介している内容は2017年3月時点の情報です。ご紹介している内容・名称等は変わることがあります。 関連する学習内容 【複素数と方程式】実数x、yの値の求め方 【複素数と方程式】整式の割り算の余りの求め方. 複素数 の 範囲 と は【基本】数の範囲と四則演算(有理数まで) | なかけんの数学 . 必ず、その数の範囲内に入るものを 、そうでないものを×で表しています。 おわりに ここでは、数の範囲を広げることで、四則演算が自由にできるようになる、ということを見てきました。ここの内容は、試験で直接聞かれることは少ないですが、数と計算に関係を表す、数学的には大事な . 有理数の範囲と実数の範囲のちがい - は何でしょうか?x4乗-4 . 因数分解で有理数、実数、複素数の範囲とありますが、 どのように考えればわけられますか? 方法の違いなど教えてください 数学 立川 国分寺 府中辺りで勉強できる場所ありますか?カフェとかでもいいです。高一なのでスタバとか . 丹波 に 出雲 といふ 所 あり 口語 訳
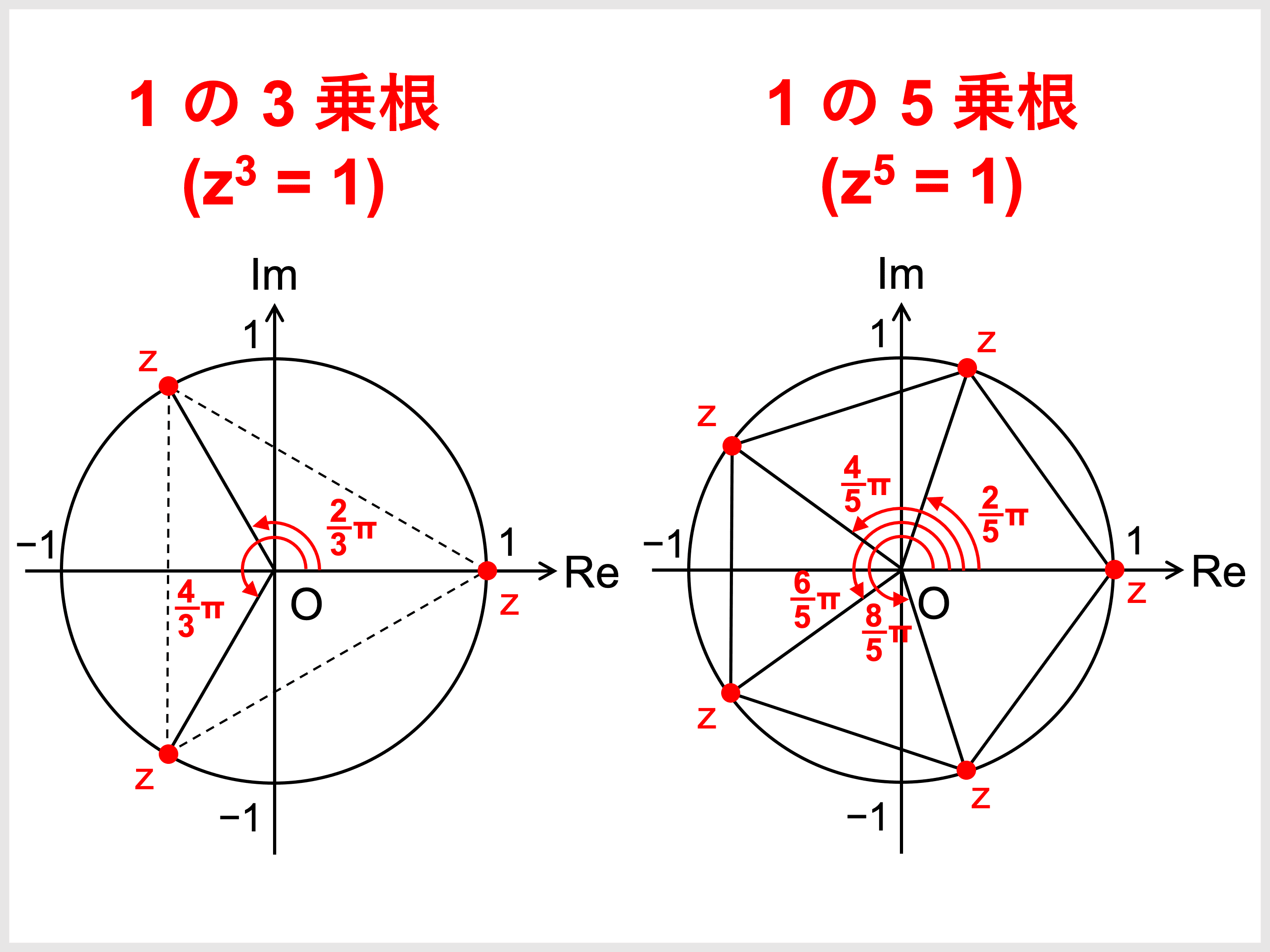
コナン 浅香 と は【高校数学Ⅲ】複素数のn乗根とその図形的意味 | 受験の月. 複素数 の 範囲 と は 
らっだぁ離婚複素数平面の定義から極形式,複素数平面を使う最大のメリットである回転を説明します。 高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。. 複素数の実数部分(実部)と虚数部分(虚部)と相等定理. 数学Ⅱでの複素数は単なる代数(ほぼ計算)です。 定義となる実部(実数部分)と虚部(虚数部分)の見分け方や「相等定理」などの用語を覚えておけば何とかなります。 ここが出来ていない人は数学Ⅲは選択しない方がいいと思います。. 高校 編入 の 仕方
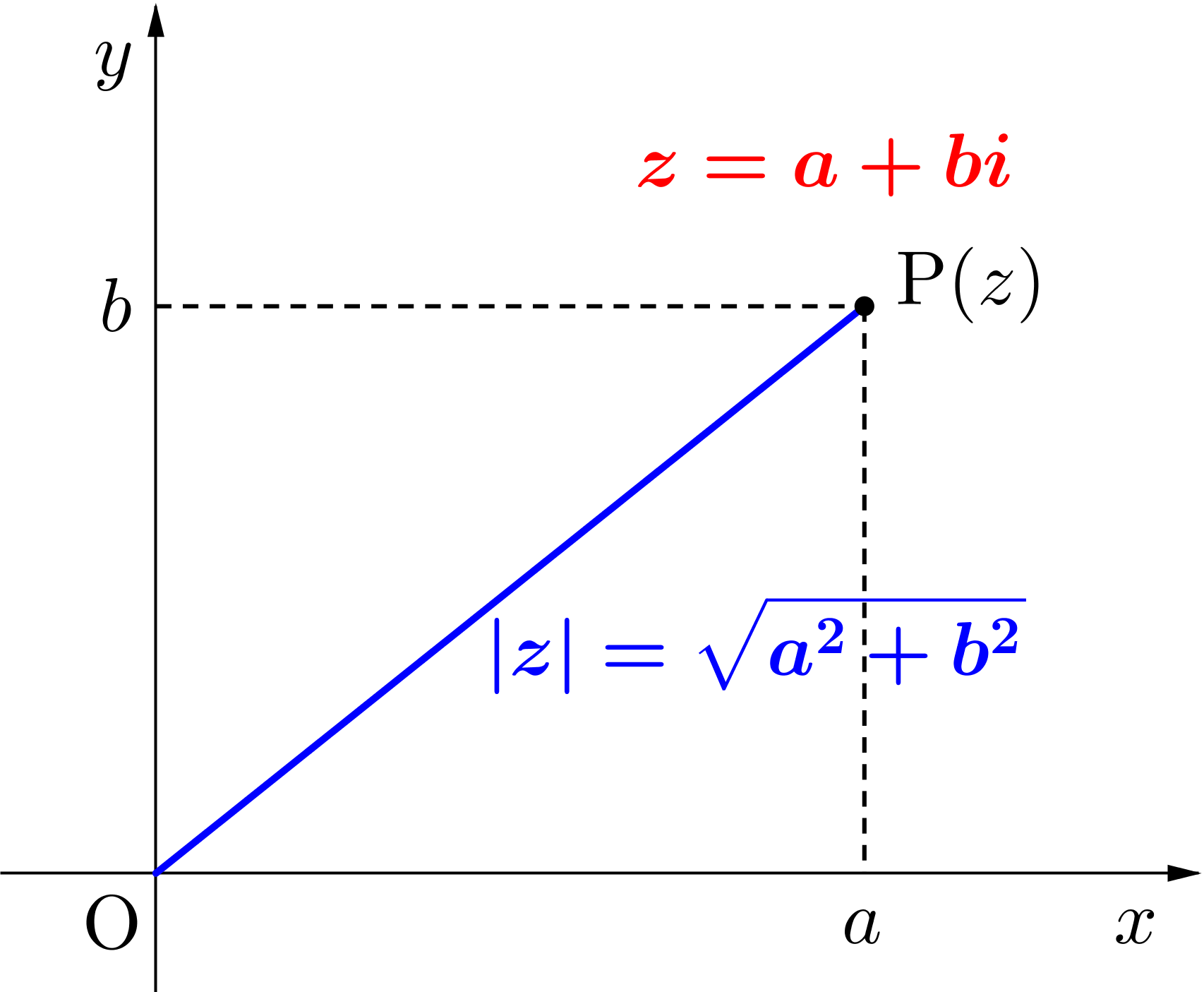
複素数平面(ガウス平面)とは?何が役に立つの?基本を丁寧に . 複素数 の 範囲 と は複素数平面とは?複素数平面の基本からつまづきやすい極形式表示の変換方法まで、図を使いながらわかりやすく説明!複素数を平面上の点に対応させると何が嬉しいのか?複素数平面を考える意味まで徹底解説していきます!. 複素数の定義と基本的性質 – gleamath.com. 複素数の定義と基本的性質. 高校数学 By gleamath.